[15] Deep Learning - Optimizer
Optimizer
network에 사용할 수 있는 optimizer의 종류는 다양하다. 기본적으로 알려져 있는 경사 하강법이 그 예다. 경사 하강법 이외에도 모멘텀 최적화 , 네스테로프 가속 경사 , AdaGrad , RMSProp , Adam , Nadam 등 다양한 optimizer가 존재한다.
모멘텀 최적화 (Momentum Optimization)
공이 경사를 따라 내려갈 때 , 가속도에 의해 종단 속도에 도달할 때까지 속도는 빠르게 가속될 것이다. 모멘텀 최적화는 이러한 원리를 이용한다. 기존의 경사 하강법에서는 한 스텝 한 스텝씩 차근차근 경사를 내려갔다면 , 모멘텀 최적화의 경우는 경사에 공을 굴리는 것과 같이 경사를 내려간다.
모멘텀 최적화는 이전 경사가 어떤 값이었는지를 고려해 경사를 내려간다. 경사 하강법의 경우 한 스텝씩 내려가므로 이전에 얼마나 경사를 내려갔는지는 중요하지 않다. 하지만 모멘텀 최적화는 이를 고려한다. 모멘텀 최적화는 반복하면서 현재 경사에 학습률 lr을 곱한 후 , m (모멘텀 벡터)에 더하고 이 값을 뺴는 방식으로 weight를 갱신한다. 즉 경사가 가속도로 작용되는 것이다. 여기에 마찰저항을 구현하기 위해 새로운 parameter인 β를 사용한다. 위의 아이디어를 식으로 표현하면 다음과 같다.


모멘텀 최적화는 경사 하강법에 비해 평탄한 지역을 비교적 빨리 탈출할 수 있도록 도와준다. 또 경사 하강법과 달리 모멘텀 최적화는 공을 경사에서 굴리는 것과 같이 최적점 , 즉 바닥에 도달할 때까지 점점 더 빠르게 내려간다. 배치 정규화를 사용하지 않는 경우 , scale이 크게 다른 입력을 받을 수 있다. 이런 경우 모멘텀 최적화가 도움을 줄 수 있다.
keras에서 모멘텀 최적화를 구현하는 방법은 다음과 같다.
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
#모멘텀은 일반적으로 0.9
모멘텀 parameter를 튜닝해야 할수도 있다. 하지만 대부분 0.9에서 잘 작동한다.
네스테로프 가속 경사 (Nesterov accelerated gradient)
네스테로프 가속 경사는 모멘텀 최적화의 일종으로 , 기본 모멘텀 최적화보다 일반적으로 빠르다. 모멘텀으로부터 나왔기 때문에 NAG 또는 네스테로프 모멘텀이라고 불린다.
네스테로프 모멘텀은 기본 모멘텀 최적화의 식과 일정 부분만 다르다. 기존의 모멘텀 최적화에서 목적함수의 경사를 현재 가중치를 통해서 정했다면 , 네스테로프 모멘텀은 모멘텀의 방향으로 weight + βm 에서의 경사를 계산한다. 네스테로프 모멘텀의 식은 다음과 같다.


일반적으로 모멘텀 벡터가 최적점을 가리킬 것이므로 본래 위치의 경사보다 한 발짝 더 나아간 곳의 경사를 사용하는 것이다. 이러한 조그만 이득이 눈덩이처럼 불어나서 일반적인 모멘텀 최적화보다 네스테로프 모멘텀이 더 빠르게 된다.
keras에서 네스테로프 모멘텀은 다음과 같이 사용할 수 있다.
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9 , nesterov=True)
# nesterov=True 를 통해 네스테로프 모멘텀을 사용 할 수 있다.
AdaGrad
먼저 AdaGrad의 식을 살펴보자.


첫 번째 식은 경사의 제곱을 벡터 s에 누적하는 식이다. 중간의 ⊗ 기호는 원소별 곱셈을 의미한다. si는 가중치 wi에 대한 비용 함수의 편미분 값을 제곱해서 누적하는 것이다. 비용 함수가 만약 i번쨰 차원을 따라 가파르다면 si는 반복을 진행하면서 누적되고 점점 더 커질 것이다.
두 번째 식은 경사 하강법과 유사하다. ⊘ 기호는 원소 별 나눗셈을 의미한다. 기존의 경사 하강법과 다른 점은 뒤쪽의 루트 값으로 경사 값을 나누어 scale을 조정한다는 점이다.
따라서 학습률이 감소되지만 , 경사가 완만한 차원보다 가파른 차원에 대해 더 빠르게 감소되고 이를 적응적 학습률이라고 한다. 이 적응적 학습률은 global optimum으로 계속해서 움직이도록 도움을 준다. AdaGrad는 간단한 문제들에 대해서는 잘 작동하지만 , 훈련 시 너무 일찍 멈춰버리는 경우가 발생한다. 학습률이 과하게 감소되어 global optimum에 도달하기 전에 멈춰버리는 것이다. 따라서 AdaGrad는 간단한 문제에는 사용할 수 있지만 , deep 한 network에 사용하기에는 좋지 않다.
keras에서 AdaGrad는 다음과 같이 사용할 수 있다.
optimizer = keras.optimizers.Adagrad(learning_rate = 0.001)
RMSProp
AdaGrad의 문제점을 RMSProp은 가장 최근 반복의 경사만을 누적하는 방식으로 해결했다. RMSProp의 식은 다음과 같다.
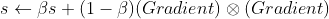
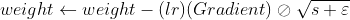
보통 감쇠율인 β는 0.9로 둔다. 기본값으로 두어도 잘 작동하므로 크게 튜닝할 필요는 없다.
keras에서 RMSProp을 다음과 같이 사용할 수 있다.
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
#rho는 위의 식의 베타를 의미한다
간단한 문제에만 의미 있게 사용이 가능했던 AdaGrad와 달리 RMSProp은 성능이 괜찮게 나와 선호되었던 optimizer 였다.
Adam & Nadam
Adam은 적응적 모멘트 추정 (adaptive moment estimation)을 의미한다. Adam은 모멘텀 최적화와 RMSProp의 아이디어를 합친 것으로 식에 이러한 아이디어가 반영되어 있다.

식을 살펴보면 모멘텀 최적화와 비슷한 부분과 RMSProp과 비슷한 부분이 보인다. 논문에서 소개하는 prameter들의 기본값은 α = 0.001, β1 = 0.9, β2 = 0.999 , ε =10^-8이다. ε의 경우 아주 작은 값을 택해 안정된 계산이 이루어질 수 있도록 한다.
keras에서 Adam을 다음과 같이 사용할 수 있다.
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9 , beta_2=0.999)
#위의 식에서 알파가 lr을 의미한다
Adam에서 나온 2개의 optimizer가 존재한다. 바로 Nadam과 AdaMax이다.
AdaMax
AdaMax는 Adam이 l2 norm으로 parameter 업데이트 scale을 낮췄다면 AdaMax는 L-Infinity Norm을 사용한다. 이름에 Max가 들어가는 이유가 바로 이 때문이다. AdaMax는 경우에 따라 Adam 보다 안정적이기도 하다. 하지만 일반적으로 Adam의 성능이 더 좋으므로 , 대부분 Adam을 사용해보고 그 이후에 결과가 마음에 들지 않는다면 AdaMax를 사용한다. 논문에서 소개하는 AdaMax의 식은 다음과 같다.

Nadam
Nadam은 Adam에 네스테로프를 더한 optimizer다. Adam , Nadam , RMSProp와 같은 적응적 최적화 방법이 성능도 좋고 속도도 빠른 것은 사실이다. 하지만 언제나 그렇지는 않다. 데이터 셋의 특징에 따라 모델의 optimizer도 달라져야 한다. 모델에서 어떤 optimizer에 대해 성능이 좋지 않다면 다른 optimizer를 사용하는 것도 고려해보아야 한다.
정리
지금까지의 모든 최적화 기법들은 야코비안 , 1차 편미분에 의존하는 기법들이다. 2차 편미분을 이용한 알고리즘들이 있지만 이러한 알고리즘들은 DNN에서 사용하기에는 어렵다. 편미분 해야 하는 계산 양이 어마어마하게 많아지기 때문이다. 이를 감당할 메모리도 문제고 , 속도가 너무 느리다는 것도 문제다.
고려할 수 있는 optimizer 선택 ( 1~3점 )
- SGD / 속도 : 1 / optimum 품질 : 3
- 모멘텀 최적화 / 속도 : 2 / optimum 품질 : 3
- 네스테로프 최적화 / 속도 : 2 / optimum 품질 : 3
- AdaGrad / 속도 : 3 / optimum 품질 : 1
- RMSProp / 속도 : 3 / optimum 품질 : 2 ~ 3
- Adam / 속도 : 3 / optimum 품질 : 2 ~ 3
- Nadam / 속도 : 3 / optimum 품질 : 2 ~ 3
- AdaMax / 속도 : 3 / optimum 품질 : 2 ~ 3
ref
- "Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd Edition"
- Diederik P. Kingma, Jimmy Ba , Adam: A Method for Stochastic Optimization
'코딩 > 데이터 분석 이론 & 응용' 카테고리의 다른 글
| [17] Deep Learning - Regularization (0) | 2022.01.27 |
|---|---|
| [16] Deep Learning - Learning Rate Scheduling (0) | 2022.01.25 |
| [14] Deep Learning - Transfer Learning & Pre-training (0) | 2022.01.23 |
| [13] Deep Learning - Gradient clipping (0) | 2022.01.20 |
| [12] Deep Learning - Batch normalization (0) | 2022.01.19 |


