[6] Deep Learning - Neural Network
Neural Network
Neural Network의 역사는 과거부터 시작되었다. 사람의 뇌를 본뜨고자 하는 아이디어가 제시되었고 , 뉴런을 만들어 뇌의 구조를 흉내 내고자 하였다.

뉴런은 axon , 축삭돌기를 통해 활동전위를 전달한다. 이러한 뉴런의 구조를 본떠 입력을 받는 부분과 출력을 내보내는 부분이 존재하도록 객체를 만들었다. 위의 그림은 뉴런과 객체를 비교한 그림이다. 두 그림 모두 입력과 출력에 대한 부분이 존재하는 것을 확인할 수 있다. cell body에 들어온 입력에 대해 어떠한 함수에 대입해 계산하고 그 결과를 출력으로 내보내는 구조이다. 뉴런이 모여있으면 Neural Network이므로 , Neural Network는 뉴런의 집합이라고 생각할 수 있다. Neural Network는 80 ~ 90년대에 자주 사용되던 알고리즘 이었는데 , 90년대 이후에 사장되었다. 문제를 잘 해결하지 못했기 때문이다.

계산이 이루어지는 과정은 다음과 같다. 뉴런은 들어오는 Input에 대해 서로 다른 가중치를 곱하여 bias term과 함께 더한다. 이후 Activation function을 거치는데 이게 사람의 뉴런을 묘사한 가장 큰 부분이다. 뉴런에서는 자극이 들어오면 반응이 나오는데 언제나 내보내는 것은 아니다. 역치를 넘어야 반응 즉 response를 보내주는데 이걸 묘사하기 위해 Activation function을 사용한다. 아래는 Activation function의 예시인 sigmoid activation function이다.

sigmoid activation function은 모든 x값에 대하여 y값이 0 ~ 1 사이의 값을 가진다. 또한 모든 구간에서 미분 가능하고 x값과 y값이 함께 증가하는 함수다. 따라서 위에서 더한 값을 Activation function안에 넣을 때 , sigmoid activation function을 사용하게 된다면 위의 함수에 넣게 되는 것이다. 도출되는 값은 무조건 0 ~ 1 사이의 값으로 나오게 될 것이다. 좀 더 세부적으로 보자면 들어간 값이 0보다 작다면 0.5 보다 작게 나올 것이고 , 0보다 크다면 0.5보다 크게 나올 것이다.
sigmoid activation function 사용했을 때 , 가장 큰 장점은 universal approximation , 즉 세상에 존재하는 어떠한 함수던지 일정 수 이상의 뉴런을 사용하면 모두 만들 수 있다는 것이다.

위의 그림은 Multilayer Neural Network를 간단하게 표현한 그림이다. Multilayer Neural Network라고 하고 Deep Neural Network라고도 한다. 이는 모두 layer가 많다는 것을 의미하고 layer가 많다는 것을 deep 하다라고도 이야기한다. 또한 위처럼 모든 뉴럴과 뉴럴 사이에 connection이 있는 Neural Network를 Fully connected Neural Network라고 한다. layer의 종류는 3가지로 input layer , hidden layer , output layer가 있다. 즉 deep 하다는 의미는 hidden layer의 수가 많음을 의미하고 이는 좀 더 복잡한 문제를 유추할 수 있다는 것을 의미한다.
regression이던 classification이던 어떠한 function을 찾는 것이 목표일 것이다. classification이라면 Decision boundary를 찾는 것이 목표일 것이고 regression이라면 함수 식 자체를 찾는 것이 목표일 것이다. 문제가 복잡하고 어렵다는 것은 function이 어렵다는 것을 의미하고 이를 위해서는 deep 한 Neural Network가 필요하다는 것이다.
Input layer에서 뉴럴의 개수를 결정하는 것은 Input data의 차원과 관련 있고 , Output layer의 뉴럴의 개수는 문제 정의를 어떻게 하였는가에 따라 달라진다. 예시로 이미지가 들어왔을 때 , 개인지 고양이인지 구분하는 문제를 살펴보자. Input data는 10 * 10 픽셀의 사진이다. 그렇다면 한 픽셀 픽셀이 Input으로 들어오므로 Input 뉴럴의 개수는 100개가 될 것이다. 개인지 고양이인지 2개로 구분하므로 Output 뉴럴의 개수는 2개가 될 것이다. 각각이 고양이 score , 개 score 라면 두개를 비교해보고 높은 쪽을 답을 내면 될 것이다.
Input 뉴럴과 Output 뉴럴의 개수는 위와 같이 정하면 된다. 그렇다면 hidden layer의 경우는 어떻게 해야 할까. hidden layer의 수와 안에 들어가는 뉴럴의 개수는 모두 hyper parameter다. 즉 사람이 정해야 한다는 것이다. 그렇다면 뉴럴의 수가 많을수록 복잡한 문제를 해결할 수 있으니까 무조건 많은 모델이 좋을까라고 생각하면 아니라는 것이다. layer의 수가 많고 뉴럴의 수가 많아질수록 Overfitting의 가능성은 높아진다. 그래서 여러 Network 구조를 실험해보고 Training 에러와 Test 에러 사이의 적절한 지점을 찾아야 할 필요가 있다.
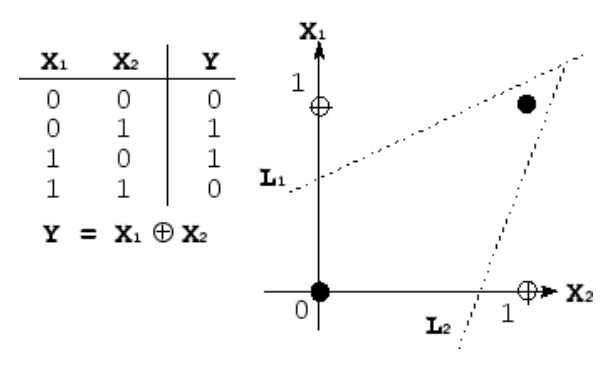
대표적인 비선형 분류 문제인 XOR 문제이다. 각각의 X1과 X2에 대해 XOR 한 결과를 좌표평면상에 표현하였고 이를 구분하는 경계를 찾는 문제이다. 위의 그림에서 확인할 수 있듯이 선형 경계로는 분류하게 어려운 것을 확인 할 수 있다. 따라서 XOR 문제의 분류 경계선은 부드러운 비선형 구조로 나타내야 한다.
앞서 Neural Network를 통해 어떠한 function도 다 만들 수 있다고 하였다. 그렇다면 위의 부드러운 비선형 경계도 Neural Network를 통해 만들 수 있을 것이다. 만약 Neural Network에서 activation function이 없다면 어떻게 될까. activation function이 없으므로 계속 선형식에 값을 대입하게 될 것이고 결국 Output 역시 선형 식의 결과가 나오게 될 것이다. activation function 없이 진행한 Neural Network는 결과로 선형식을 도출하였고 , 이를 통해서는 위의 간단한 XOR 문제도 해결하지 못한다. 즉 Neural Network에 있어서 activation function이 필요한 이유는 위처럼 non-linear 한 function을 표현하기 위함이다.
결과적으로 Neural Network를 통해 XOR 문제를 해결하면 다음과 같이 나올 것이다.
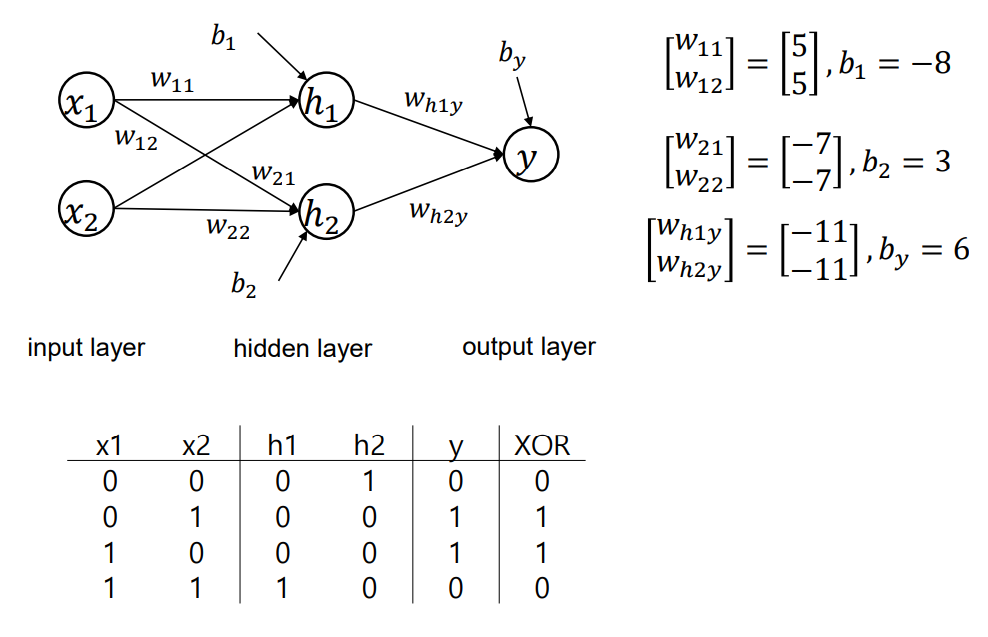
각 layer를 거치면서 입력된 데이터들을 통해 weight를 학습하고 Training data에 대해 식을 만족하는 function에 대해 weight와 bias 조합이 매우 다양하게 나올 것이다.
XOR 문제가 아닌 좀 더 복잡한 Multiclass classification 문제를 통해 살펴보자.
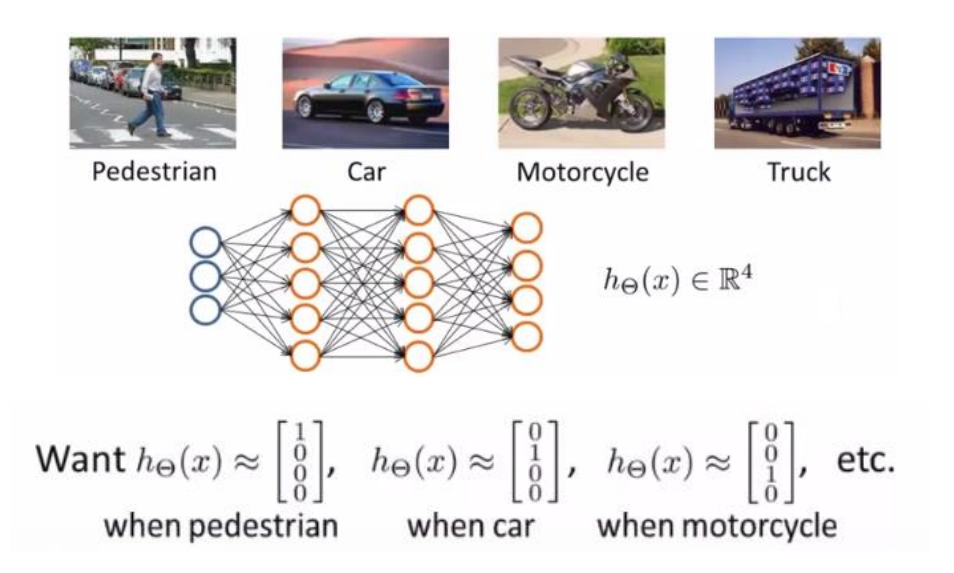
만약 위의 그림과 같은 예시라면 , Output 뉴럴의 수는 4개가 될 것이다. 만약 0.001 , 0.001 , 0.997 , 0.001이라는 4개의 Output이 나왔다면 가장 값이 높은 0.997에 해당되는 Motorcycle로 분류하게 될 것이다. 앞서 이야기 한 Output 뉴럴의 수는 문제 정의에 따른 다는 이야기가 이러한 내용이다.
그렇다면 Neural Network에서 training data로부터 weight와 bias를 어떻게 학습할 수 있을까. 이때 사용하는 방법이 Error backpropagation이다. 에러를 계산해 뒤로 넘기겠다는 의미이다. 에러는 당연하게도 모델의 최종 Output 값과 실제값의 차이를 계산해야 구할 수 있다. 그렇게 나온 에러를 다시 Output layer부터 거꾸로 올려 보내겠다는 것이다. 즉 에러가 작아지는 방향으로 학습을 하겠다는 것이다. 에러의 경사가 낮아지는 방향으로 갈 것인데 , 에러에 대한 경사는 편미분을 통해 구할 수 있다.
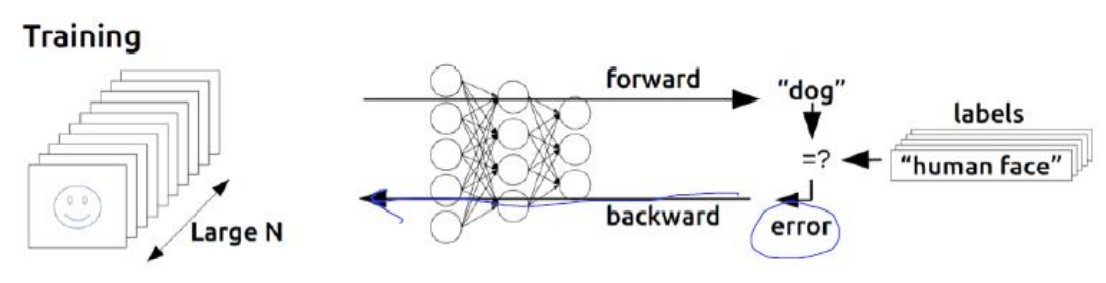
즉 에러에 대하여 경사 하강법을 사용하는 것이다. 이러한 과정을 통해 에러를 다시 올려 보내는 과정에서 편미분을 곱해나가기 위해 Chain rule을 사용한다.
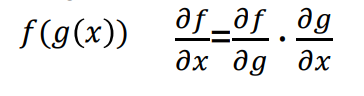
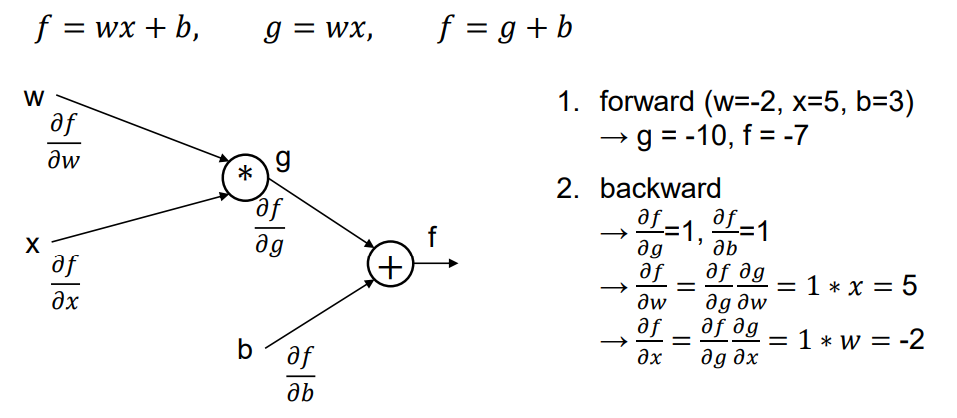
마지막 hidden layer의 weight를 W2라고 하자. 그렇다면 W2는 에러(E)와 바로 맞닿아 있으므로 편미분 E/W2가 가능하다. 하지만 한 칸 앞쪽의 hidden layer의 weight인 W1은 E와 맞닿아 있지 않아 바로 편미분이 불가능하다. 이때 Chain rule을 사용해 E/W2를 구할 수 있다. 즉 W2는 W1을 통해 표현되는 함수라고 볼 수 있기 때문에 Chain rule을 사용해 E/W2 즉 에러와 W2와의 관계를 구할 수 있는 것이다.
이러한 과정을 계속 거쳐 앞쪽의 Input layer들의 뉴럴까지 반복한다는 것이다. 그렇다면 이는 맨 앞쪽의 Input에 대한 에러를 편미분 할 수 있다는 것이고 , 이를 통해 경사 하강법 사용이 가능하다.
'코딩 > 데이터 분석 이론 & 응용' 카테고리의 다른 글
| [8] Deep Learning - Perceptron (0) | 2022.01.12 |
|---|---|
| [7] Deep Learning - CNN (0) | 2022.01.09 |
| [5] Co-Occurrence Networks Analyzing (0) | 2022.01.08 |
| [4] Latent Semantic Analysis & SVD (1) | 2022.01.08 |
| [3] Predicting Forest Cover with Decision Trees (0) | 2022.01.07 |



