[4] Latent Semantic Analysis & SVD
Latent Semantic Analysis
자연어란 , 기계어나 프로그래밍 언어가 아닌 인간이 사용하는 언어를 의미한다. 자연어 기반의 데이터 즉 텍스트 데이터 들은 정형화되지 않은 비정형 데이터다. 정형화 데이터란 , 테이블 형식으로 표현이 가능하고 SQL을 이용한 query를 통해 기준에 맞는 데이터들을 확인할 수 있는 데이터를 이야기한다. 비정형 데이터는 이러한 특징이 없기 때문에 데이터를 다루는 데에 있어서 다른 방법을 사용해야 한다.
Latent Semantic Analysis (LSA)란 , 각 문서에 포함된 단어들의 관계를 통해서 그 문서를 이해하고자 하는 방법이다. LSA의 가장 기본적인 목표는 관련된 콘셉트를 잘 뽑아내는 것이며 , importance score를 통해 얼마나 잘 표현하는 지 표현한다.
LSA를 사용한 하나의 예시이다. LSA를 사용한 결과 , LSA는 "요리"라는 단어와 "요리사"라는 단어 사이에 높은 관련성이 있다고 판단하였다. 또한 문서와 문서 사이를 확인한 결과 "요리 레시피 책"과 "요리사의 자서전"이 높은 관련성이 있었다. 이처럼 LSA는 문서와 문서 , 단어와 단어 , 문서와 단어 사이의 관련성을 확인할 수 있다. 따라서 높은 관련성을 가지는 데이터들로 하여금 노이즈를 솎아낼 수 있고 , 불필요한 단어들은 삭제하고 의미 있는 단어들은 합병해 의미 있는 형태로 만들 수 있다는 것이다.
그렇다면 단순하게 생각해서 어떠한 문서에 가장 많이 등장하는 단어가 그 문서를 대표할 수 있을까. 그렇지 않다는 것이다. 만약 어떠한 문서에 관사인 A나 The가 많이 나왔다고 해서 이 단어들이 문서를 대표한다고 생각할 수는 없을 것이다. 또한 co- occurrences 즉 동시 출현한 단어들이나 , 자주 등장하는 단어가 그 문서를 대표한다는 방법은 너무 단순하다. LSA는 빈도수가 아닌 단어와 단어 사이의 similarity를 제공하기 때문에 더 깊게 이해 가능하다. 이러한 similarity 측정은 문서의 set중에서 의미 있는 query terms을 찾거나 , 문서를 주제로 묶거나 , 그 문서를 표현하는 관계가 있는 단어를 찾아낼 수 있다.
이를 위해서는 corpus의 raw-text data들을 document-term matrix로 바꿔야 한다. matrix의 column이 의미하는 바는 term을 의미하고 , row는 문서를 의미한다. 그리고 안의 요소는 그 column의 term이 그 문서에 얼마나 중요한지를 의미한다. 그렇다면 어떠한 term이 어떠한 문서에 얼마나 중요한지 표현할 수 있는 방법이 있어야 할 것이다. 많이 등장했다고 중요한 term이라는 단순한 기준이 아닌 중요도를 표현할 수 있는 다른 기준이 필요하다.
중요도는 TF-IDF 방식으로 표현한다. TF-IDF 식은 다음과 같다.

TF-IDF는 중요도를 Term Frequency * Inverse Document Frequency로 표현한다. Term Frequency를 통해서는 문서에 존재하는 전체 term들 중 해당 term의 출현 빈도를 확인한다. 즉 문서에 많이 등장하는 단어일수록 중요할 것이라는 기본적인 콘셉트를 살려서 가는 것이다. 이 Term Frequency만 가지고 하면 앞의 word counting과 다를 바가 없다. 따라서 뒤에 Inverse Document Frequency를 추가하였다. Inverse Document Frequency의 분모는 그 term이 등장한 문서의 개수이고 , 분자는 전체 문서의 개수이다. 예를 들어 The 같은 관사는 모든 문서에 등장할 것이다. 그렇다면 문서가 100개 있다고 가정했을 때 Inverse Document Frequency는 log(100/100) 으로 나올 것이고 , 이를 통해 중요하지 않다는 판단이 가능하다. 즉 Inverse Document Frequency는 어떤 단어가 그 문서에 있어서 중요한 단어라면 그 문서에만 등장할 것이다 라는 아이디어로 표현한 식이다. 만약 그 단어가 다른 문서에도 빈번하게 나왔다면 이 문서의 특징을 나타내기에 좋지 않은 단어구나라고 판단한다는 것이다. Inverse Document Frequency는 Term Frequency 처럼 표현할 경우 Scale이 너무 커지기 때문에 log Scale을 취해 계산한다.
그렇다면 왜 log Scale을 취하였는지에 대해서도 생각해 볼 수 있다. 그 이유는 corpus안에서 단어 빈도의 분포가 exponentially 하게 분포되어있기 때문이다. 즉 linear 하지 않다는 것이고 , 이는 많이 등장하는 단어는 정말 많이 등장하고 적게 등장하는 단어는 정말 적게 존재한다는 것을 의미한다. 이러한 분포를 linear 하게 풀어내기 위하여 log를 사용한 것이다. 예를 들어 , 가장 많이 등장하는 단어는 보통 단어에 비해 10배 더 많이 나오고 가장 적게 등장하는 단어는 보통 단어에 비해 10배 더 작게 나온다는 것이다. log를 통해 Inverse Document Frequency를 linear 하게 풀어내 어느 한쪽에 치우치지 않은 결과가 나오도록 한 것이다.
위의 방식에 따라 document-term matrix을 만든 이후 , 분석은 LSA에서 이루어진다. LSA는 두 가지 특징이 존재한다. 첫 번째는 각각의 문서는 단순하게 단어들이 들어있는 가방으로 생각하겠다는 것이다. 즉 단어들 사이의 순서나 문장 구조등 다양한 요소는 고려하지 않겠다는 의미이다. 즉 set , 집합 구조로 문서 안의 단어들을 표현한 것이다. 두 번째는 동음이의어는 처리하지 못한다는 점이다. 예를 들어 하늘에서 내리는 "눈"과 사람의 "눈"을 LSA는 구분할 수 없다는 것이다.
이러한 점이 바로 LSA의 한계이다. LSA는 단어들의 동음이의어 , 문맥 , 부정형이 어디에 존재하는지 고려하지 않아 이러한 부분들을 확인할 수 없다. 따라서 LSA는 문서를 잘 표현하는 단어를 찾는 기본적인 알고리즘이라고 생각하면 된다.
document-term matrix는 M * N 행렬이다. M은 문서의 수 , N은 term의 수다. 이제 document-term matrix을 분석해야 하는데 이때 사용할 수 있는 선형대수적 방법이 SVD , 특이값 분해다.
Singular Value Decomposition (SVD)

SVD는 하나의 matrix를 3개의 matrix로 나누는 방법이다. 각각 U , S , V^T로 나뉘게 된다. 당연하게도 차원을 유지하지 않는 경우에는 완벽하게 같아질 수는 없다. 그래서 위의 기호가 = 이 아닌 ≈인 것이다. 각각의 matrix는 다음과 같다.
- U : m * k matrix , row가 orthonormal basis , 문서 공간을 표현
- S : k * k matrix , diagonal matrix이고 concept에 대하여 표현
- V^T : k * n matrix , column이 orthonormal basis , term 공간을 표현
k를 우리가 정하여 사용하기 떄문에 원본 matrix가 돌아오는 형태가 아니게 되는 것이다.

본래의 SVD는 다음과 같고 , 위의 그림에서 diagonal에 있는 값이 Singular Value가 된다.
SVD에는 다양한 변형이 있는데 그중 Truncated SVD를 살펴본다.
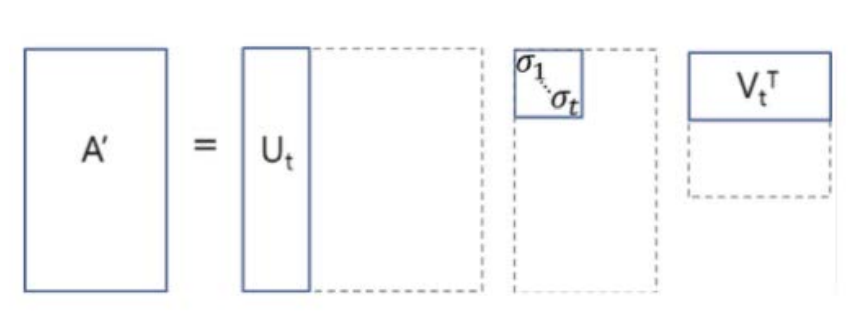
Truncated SVD는 diagonal을 통해 Singular Value가 나올 때 , N개 중에서 값이 큰 순서대로 t개를 고르는 방식이다. 즉 영향력이 큰 순서대로 고르는 것이다. 이 선택된 Value에 매칭 되는 matrix의 column이 있을 것이고 , 이렇게 3개를 곱하면 원본 matrix가 근사하게 복원된다. 즉 근사하게 복원된 matrix인 A'이 존재하게 되는 것이고 차원을 줄일 수 있다는 것이다. 아래 그림을 통해 더 자세히 살펴보자.
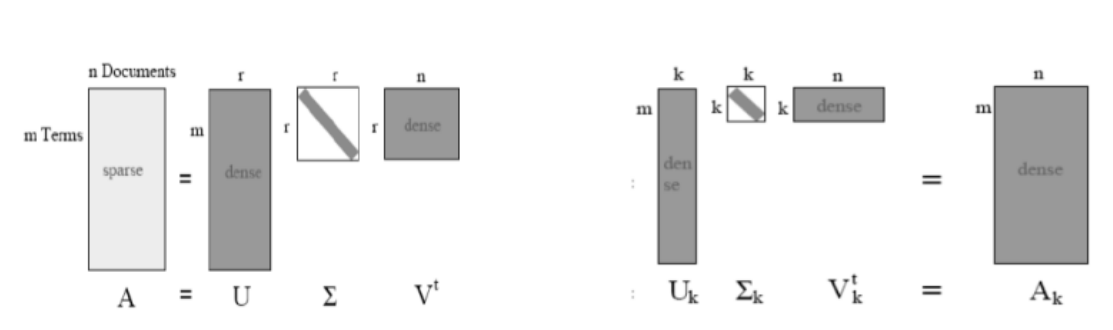
완벽하게 복원하는 경우와 비교했을 떄 , 결과를 확인하면 보다 dense 하게 나오는 것을 확인할 수 있다. LSA에서 원하는 것은 오른쪽의 Truncated SVD 다. 위에서 보았듯이 k를 고르고 , 그를 통해 3개의 행렬곱을 만드는 과정을 통해 근사화된 matrix를 만들 수 있다. 원본은 sparse 했을 지라도 , 근사화된 matrix는 dense 하다. 이를 통해 dense 하게 정리할 수 있다는 것이고 분석에 좀 더 용이하다는 것이다.
document-term matrix를 가지고 k를 선택한다. 문서의 개수가 M개 , term의 개수가 N개 라면 대부분은 M > N이다. 왜냐하면 문서는 가능한 만큼 계속 넣을 수 있지만 , 사용되는 term의 수는 한정적이기 때문이다. 사전에 있는 모든 단어를 다 모아도 문서를 무한하게 넣는 다면 언제 가는 M > N 인 순간이 오게 된다. 그래서 결과는 low-rank approximation matrix가 나오게 된다.

각 공간에 존재하는 Vector들은 다음과 같은 의미를 가진다.

이 3가지 공간 중 concept space에 존재하는 Singular Value는 각 concept에 대한 weight를 의미한다. 즉 term과 문서 사이의 관계에 대한 weight이다.
각 matrix에 대한 자세한 설명은 다음과 같다.
- V : n * k matrix (V^T가 k*n이었기 때문에) / row는 term , column은 concept에 대응/ 이 matrix가 정의하는 바는 term space와 concept space 간의 mapping / 각각의 포인트가 k 차원의 벡터고 concept을 가지게 된다.
- U : m * k matrix / row는 문서 , column은 concept에 대응 / 이 matrix가 정의하는 바는 문서 space와 concept space를 mapping
- S : k * k matrix / single concept에 대응하는 diagonal Singular Value / 값이 클수록 중요함
TF-IDF와 SVD를 통해 앞의 과정을 모두 진행하였다. LSA를 통해서 의미 있는 정보를 추출하기 위해서는 어떤 matrix를 보아야 할까. V matrix는 term과 concept 사이에 mapping을 해주는 matrix이다. 즉 V matrix의 각 요소는 각각의 term과 concept 사이의 relevance (관련성)을 이야기한다. 따라서 V matrix를 통해 어떠한 concept에 대해 가장 관련성이 높은 term을 찾을 수 있는 것이다.
'코딩 > 데이터 분석 이론 & 응용' 카테고리의 다른 글
| [6] Deep Learning - Neural Network (0) | 2022.01.09 |
|---|---|
| [5] Co-Occurrence Networks Analyzing (0) | 2022.01.08 |
| [3] Predicting Forest Cover with Decision Trees (0) | 2022.01.07 |
| [2] K-means clustering algorithm (0) | 2022.01.06 |
| [1] Collaborating Filtering & Alternating Least Squares (0) | 2022.01.05 |



