[1] Collaborating Filtering & Alternating Least Squares
Gradient Descent Algorithm

다음과 같은 linear regression 식을 세울 때 식 h(x)는 다음과 같은 과정을 거쳐 나타낼 수 있다.

존재하는 Training Set에 Learning Algorithm을 적용하여 가설 h를 도출하고 , x값을 가설 h에 적용해 추정되는 y값을 도출한다. 만약 linear regression의 경우 가설 h는 일차식의 형태로 나타낼 수 있을 것이다.
이후 최적화는 목적함수의 값을 최소화 하는 방향으로 이루어진다. 만약 위의 linear regression의 경우는 다음과 같은 목적함수값을 최소화하는 방향으로 최적화가 이루어질 것이다.

목적함수의 값은 추정된 값과 실제 값이 크게 차이날 수록 더욱 커질 것이고 , 최적화의 방향은 위의 값을 가장 최소화하는 방향으로 이루어지므로 추정된 값이 실제값과 차이가 덜 나도록 이루어질 것이다.
위의 목적함수 J는 θ0과 θ1 , J(θ0 , θ1)로 이루어진 3차원 공간으로도 표현 가능하다.

목적함수의 값을 최소화 하는 θ0와 θ1을 찾는 것이 목표이다. 하지만 그렇다고 해서 모든 θ0 , θ1의 경우를 살펴볼 수는 없다. 따라서 Gradient Descent Algorithm (경사 하강법)을 사용한다. 경사 하강법은 θ0 , θ1의 랜덤한 포인트에서 출발하여 경사 (함수의 기울기)가 작아지는 방향으로 계속 이동해 극값에 도달하는 알고리즘이다. 이 경우 θ0과 θ1이 바뀌지 않을 때 까지 이동하며 , 변하지 않는 다면 그 지점을 극값으로 판단한다.
따라서 경사 하강법을 사용하기 위해서는 모델의 Parameter와 목적함수가 존재해야 한다. 목적함수의 편미분 값이 작아지는 방향으로 이동하기 때문이다.


경사 하강법에서의 α가 작거나 큰 경우 모두 문제가 발생할 수 있다.
- α가 작은 경우 : 한번에 적게 움직여 속도가 느리다. 때문에 느리게 극값에 도달한다.
- α가 큰 경우 : 한번에한 번에 크게 움직여 속도가 빠르다. 하지만 한 번에 크게 움직이기 때문에 발산할 수 있다.
경사 하강법으로 구한 극값이 global optimum 이라는 보장은 없다. 경사 하강법은 경사가 낮은 방향으로 이동하기 때문에 local optimum에 도달 할 수도 있다. 이런 경우 local optimum도 global optimum 만큼의 효과를 보여주기 때문에 , local optimum을 global optimum로 보고 사용해도 크게 문제되지는 않는다. Cost Function 같은 목적 함수들도 복잡해지고 Feature들의 개수도 많아지고 있기 때문에 local optimum도 global optimum 만큼의 성능을 보여준다는 것이다.
경사 하강법의 결과가 local optimum인 경우 , 만약 α값을 좀 더 알맞게 정하였다면 , local optimum이 아닌 global optimum에 도달 할 수도 있었다. 따라서 α값을 잘 정하는 것도 경사 하강법에 있어 중요하다.
Collaborating Filtering
만약 영화 플랫폼에서 영화 추천 알고리즘을 만드는데 , 가지고 있는 데이터는 고객의 정보와 그 고객이 본 영화 목록 밖에 없다고 가정해보자. 고객이 영화에 준 별점 , 리뷰 , 좋아하는 장르 등 세부적인 데이터가 없다는 것은 모델을 만드는 데에 사용되는 Feature 수가 적다는 것을 의미하고 , 의미 있는 결과를 내기 어려울 수 있다.
collaborative filtering은 고객에 대한 정확한 정보나 영화의 장르 등 세부적인 데이터를 몰라도 진행 할 수 있다. 만약 두 고객을 비교해보았을 때 , 시청한 영화의 80%가 서로 겹친다고 가정해보자. 그렇다면 둘의 영화 취향은 꽤 비슷할 것이고 추천할 영화들은 그중 한 명은 보고 한 명은 보지 않은 영화를 추천하면 된다는 것이다. 이러한 기본적인 아이디어가 collaborative filtering의 아이디어 이다.
collaborative filtering과 비슷한 알고리즘으로는 Content based recommendation이 있다.
Content based recommendation
Content based recommendation은 콘텐츠 혹은 어떠한 아이템에 대한 정보를 알고 있을 때 사용하는 알고리즘이다. 만약 영화를 추천한다면 , 영화들에 대한 정보 ( 장르 , 출연 배우 , 감독 등 )을 알고 있을 때 사용 가능한 알고리즘 이다.

만약 다음과 같은 영화들이 존재하고 영화 서비스를 이용하는 고객이 존재한다고 가정하자. 각 칸은 해당 고객이 해당 영화에 매긴 평점이다.
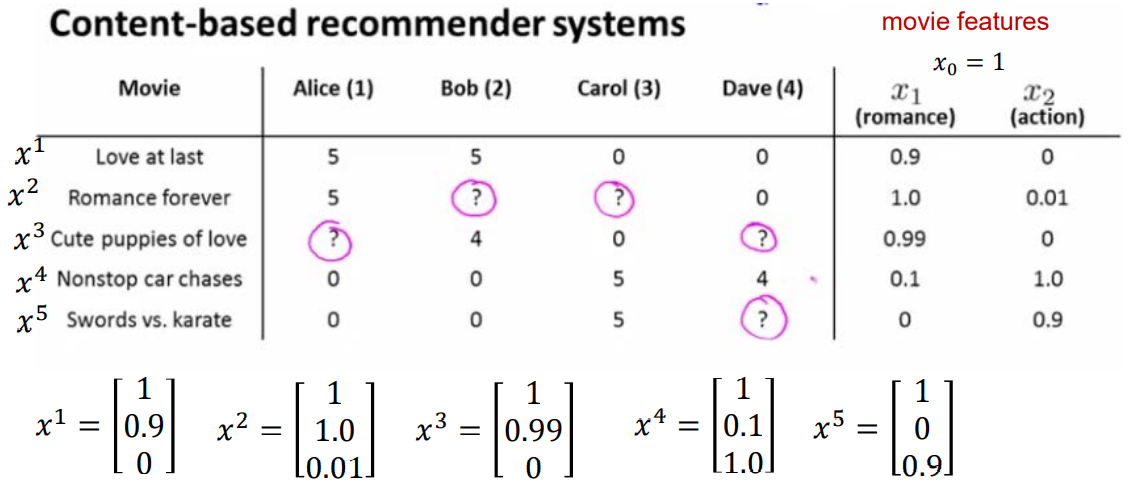
영화의 특징을 로맨스와 액션으로만 나누어 해당 영화가 어느 장르에 속하는지 행렬로 표현하였다. 즉 콘텐츠에 대한 정보가 주어진 상황이다. 장르는 2가지인데 X행렬에 장르 요소 말고 1이 붙은 이유는 행렬곱에서 bias를 살리기 위해서다. 만약 엘리스에 대한 정보 벡터가 [ 0 5 0 ]이라면 , 3번 영화에 대한 벡터인 [ 1 0.99 0 ] 과의 곱을 통해 3번 영화를 보았을 때 평점을 4.95점을 주겠구나라고 예측이 가능하다는 것이다. 이후 엘리스가 보지 않은 영화들 중 높은 평점을 줄 것으로 예상되는 영화를 엘리스에게 추천하는 것으로 영화 추천 알고리즘을 만들 수 있다.
위와 같은 추천 알고리즘을 사용하기 위해서는 고객에 대한 정보 벡터가 필요하다. 따라서 θj를 학습해야 한다.

위의 문제 해결 방법에서 r(i, j)는 영화에 점수를 매겼다면 1 , 그렇지 않다면 0으로 두고 있다. y(i, j)는 사용자 j가 영화 i에 매긴 평점이다. 또한 θj는 사용자에 대한 parameter 벡터이고 , xi는 영화 feature에 대한 벡터이다. 이를 통해 목적함수를 만들 수 있고 , 목적함수의 값이 최소화되는 방향으로 학습을 진행한다.

우리가 최소화하고 싶은 값은 위의 목적함수의 값이다. 빨간 박스의 경우 [ 추정된 평점 - 실제 평점 ] 이므로 이를 최소화해야 한다는 것에는 이견이 없다. 즉 추정된 평점을 실제값과 최대한 유사하게 만들어야 된다는 목적이 빨간 박스에 존재하는 것이다. 파란 박스의 경우 목적은 θ값을 작게 만드는 것이 목적이다. 파란 박스의 식이 하는 역할은 모델의 Overfitting을 방지하는 것이다.
만약 빨간 박스의 식만 목적 함수에 존재한다면 , Training Data에 치중한 Overfitting이 발생할 수 있다는 것이다. 그렇기에 파란색 박스의 식을 regularization term으로 두어 Overfitting을 막은 것이다. 즉 두 개의 상반된 목적을 가지고 있는 식을 목적함수에 넣어 Overfitting 되거나 Underfitting 되지 않는 최적의 지점을 찾겠다는 것이다.

따라서 위의 목적 함수를 가지고 경사 하강법을 적용하면 식은 위와 같다.
만약 영화 Feature에 대한 정보가 없다면 Content based recommendation을 사용할 수 있을까? 영화의 장르 혹은 세부적인 Feature들에 대한 정보는 실제로 찾아내기 어렵다. 그렇다면 어떻게 영화 Feature에 대한 정보 없이 영화를 추천할 수 있을까? 이에 대한 해답은 앞쪽의 collaborative filtering을 통해 해결 가능하다.
Collaborating Filtering
이번 경우에는 θ를 알고 있다고 가정하자. 즉 위쪽에는 θ를 알아내고 싶었다면 , 이번에는 영화에 대한 Feature 벡터를 알고 싶은 것이다. 만약 우리가 θ를 알고 있다면 자연스럽게 영화 Feature 벡터를 구할 수 있다.
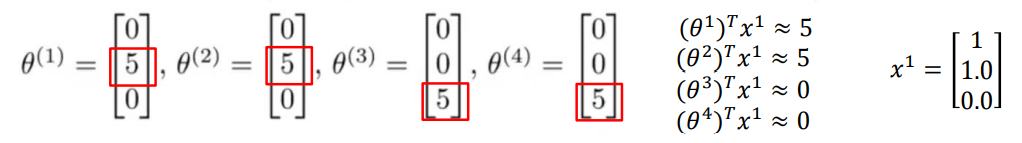
따라서 영화 Feature 벡터는 θ에 대한 정보가 있다면 값을 구할 수 있으므로 , 그에 대한 식을 목적함수에 적용하면 다음과 같다.

θ를 학습하던 목적함수와 다른 점은 학습하고 싶은 Feature에 x가 들어있다는 점이다.
정리하자면 , 사용자 정보 θ와 영화 Feature 벡터 x는 두 개 중 하나만 알면 나머지를 알 수 있는 상호 보완적인 관계에 놓여 있음을 알 수 있다.
따라서 collaborative filtering은 위의 아이디어를 통해 다음과 같은 방식으로 동작할 수 있다.
- 사용자에 대한 정보 θ , 영화에 대한 정보 x를 둘 다 모르는 상태에서 시작한다.
- 랜덤 한 값으로 θ를 세팅한다.
- 주어진 θ값으로 x를 추정한다.
- 이후 추정된 x값으로 다시 θ를 추정한다.
- θ와 x가 바뀌지 않을 때까지 3번 , 4번을 반복하고 θ와 x에 변화가 없다면 해당 값을 최종 θ와 x로 결정한다.
위의 과정을 식으로 표현하면 다음과 같다.

위의 x와 θ의 업데이트 모두 경사 하강법을 통해 이루어지며 , 이를 통해 구한 θ와 x를 통해 새로운 영화에 대한 평점을 예측할 수 있다.
위의 문제는 이와 달리 다른 방법으로도 해결할 수 있다.
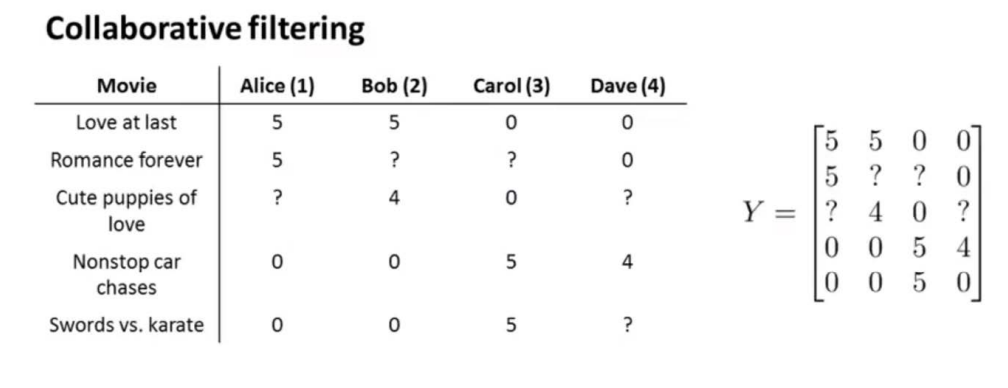
행렬 Y는 해당 사용자들이 해당 영화에 매긴 평점에 대한 행렬 이므로 풀어서 정리하면 아래와 같을 것이다.

행렬 Y를 정리하여 벡터 X와 벡터 θ로 분해할 수 있다면 , 이를 통해 문제 해결이 가능하다.
이러한 방법을 Matrix Factorization이라고 한다.
즉 Y라는 행렬이 있을 때 최대한 Y에 근접하게 나오도록 하는 벡터 X와 벡터 θ를 구하는 것이고 이를 통해서도 collaborative filtering을 구현할 수 있다.
하지만 실제 영화 혹은 음악 등의 데이터들은 위의 예시처럼 작은 경우는 드물다. 실제 대부분의 데이터들은 희소 행렬의 형태로 존재할 것이다. 이러한 경우 matrix completion algorithm을 통해 sparse matrix를 dense matrix의 곱으로 바꾸어 사용할 수 있다 (ex: N * K와 K * M). 이를 통해 나온 행렬들의 곱은 당연하게도 본래의 행렬을 복구하지는 못한다. 최대한 근사하게 찾아내는 것이 목표기 때문이다.
Matrix Factorization으로 collaborative filtering을 구현할 때의 문제는 벡터(행렬) X와 벡터(행렬) θ를 구하는 것이다. 그렇다면 어떻게 벡터(행렬) X와 θ를 구할 수 있을까? 이때 ALS ( Alternating Least Squares ) 알고리즘을 적용한다.
Alternating Least Squares
앞에서 사용자에 대한 정보 벡터 θ와 영화에 대한 정보 벡터 x를 몰랐을 때 , θ를 랜덤으로 정하고 x와 θ를 변하지 않을 때까지 업데이트했었다. 이와 비슷한 방식으로 X와 θ를 모르니까 둘 중 하나를 랜덤으로 정하고 의사 역행렬(Pseudo inverse)을 통해 다른 나머지 벡터를 구한다는 것이다. 이 역시 해당 두 행렬이 변하지 않으며 본래 행렬 Y값에 근사할 때까지 반복하고 추정치를 구해내면 된다는 것이다.
즉 랜덤 하게 세팅한 하나의 행렬로부터 다른 행렬의 값을 구하고 추정된 행렬의 값을 통해 다시 한번 다른 행렬의 값을 구하는 방식으로 진행되고 본래 행렬 값 Y와 근사한 종 수렴 값까지 진행한다는 것이다. 따라서 ALS 알고리즘을 통해 사용자와 콘텐츠에 대한 정보가 혼합되어있는 행렬에서 사용자에 대한 정보를 담은 행렬과 컨텐츠에 대한 정보가 담긴 행렬을 분리할 수 있다.
'코딩 > 데이터 분석 이론 & 응용' 카테고리의 다른 글
| [6] Deep Learning - Neural Network (0) | 2022.01.09 |
|---|---|
| [5] Co-Occurrence Networks Analyzing (0) | 2022.01.08 |
| [4] Latent Semantic Analysis & SVD (1) | 2022.01.08 |
| [3] Predicting Forest Cover with Decision Trees (0) | 2022.01.07 |
| [2] K-means clustering algorithm (0) | 2022.01.06 |



