[2] K-means clustering algorithm
K-means clustering

지도 학습에 사용하는 데이터의 경우 정답 , lable이 존재했다. Regression이나 Classification 등의 지도 학습에 사용하는 데이터 set들은 모두 Input Feature가 있고 그에 따른 lable이 존재한다. 하지만 비지도 학습의 경우 lable이 존재하지 않는다.

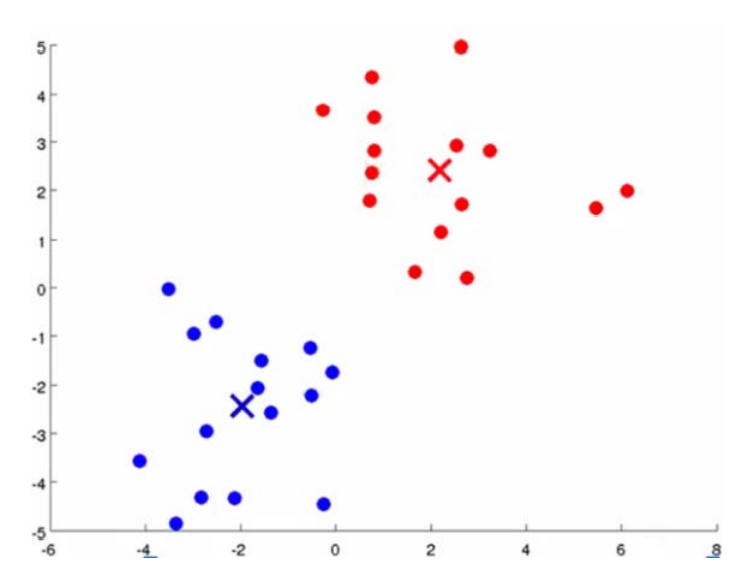
비지도 학습의 경우 lable이 없는 데이터를 사용한다. 사용하는 Training data에는 Input Feature 만이 존재한다는 것이다. K-means clustering algorithm의 경우 위처럼 lable이 없는 데이터에 lable을 붙여주는 역할을 한다. 위의 그림의 경우 2차원 상에 데이터들이 분포해 있어 사람의 눈으로도 직관적으로 Cluster를 나누고 lable을 붙여줄 수 있다. 하지만 4 , 5차원처럼 점점 고차원으로 갈수록 사람의 눈으로 나누는 것은 한계가 있을 것이다.
K-means clustering algorithm은 소셜 네트워크 분석 혹은 마트 , 백화점 품목 분류 등 다양한 곳에서 사용될 수 있다. 정답이 존재하지 않는 부분에 대해 비슷한 포인트끼리 묶는 역할을 해주기 때문이다.
K-means clustering algorithm은 다음과 같은 과정을 통해서 이루어진다.
- 분류하기로 한 Cluster의 개수인 K 만큼 Centroid를 랜덤하게 정한다.
- 각 데이터들은 Centroid까지의 거리를 계산해 가까운 Centroid의 Cluster에 속하게 된다.
- Cluster에 속한 데이터들을 통해 다시한번 Centroid의 위치를 업데이트한다.
- 각 데이터들이 속한 Cluster가 바뀌지 않을 때까지 2번 , 3번 과정을 반복한다.
위 과정을 그림으로 나타내면 다음과 같다.



더 이상 Centroid의 바뀌지 않고 , 각 Cluster에 속한 데이터들이 변함없다면 이를 K-means clustering이 수렴했다고 이야기한다.

K-means clustering에서의 parameter는 Cluster의 개수인 K가 존재한다. 따라서 K를 먼저 정한 후 , Training Set을 Input으로 사용하면 된다.

Assignment Step은 데이터들의 Cluster를 업데이트하는 단계이고 , Move Centroid Step은 Centroid들의 위치를 업데이트 하는 단계이다.
K-means clustering의 K는 parameter이므로 사용자가 원하는 숫자를 넣어 모델을 만들 수 있다. K에 매우 큰 수를 넣거나 사용하는 데이터의 Feature수가 많은 경우 , 데이터가 하나도 포함되지 않은 Cluster가 존재할 수도 있다. 실제 데이터들을 가지고 K-means clustering을 사용할 때 , Feature 수가 많기 때문에 위와 같은 경우가 발생할 수 있다. 이런 경우에는 해당 Centroid를 삭제하면 된다. 즉 삭제된 n개의 Centroid를 제외한 K-n개의 Clustering 결과를 얻었다고 볼 수 있는 것이다.
그렇다면 K-means clustering의 최적의 K는 어떻게 구할 수 있을까. K-means clustering의 K는 domain knowledge와 모델의 목적에 따라서 정하면 된다. 만약 제품 공정 시 불량 제품을 찾는 모델을 만드는 경우에는 불량과 정상 2개로 나눌 수 있을 것이다. 이처럼 K-means clustering의 최적의 K는 정해져 있지 않다.
K-means clustering에서 Centroid의 시작 위치를 정하는 initialization 방법들도 다양하게 존재한다. 대표적인 initialization 방법은 Random initialization이다.
Random initialization 방법은 n개의 데이터들 중 K개를 무작위로 뽑아 초기의 Centroid 위치로 사용하는 방법이다.
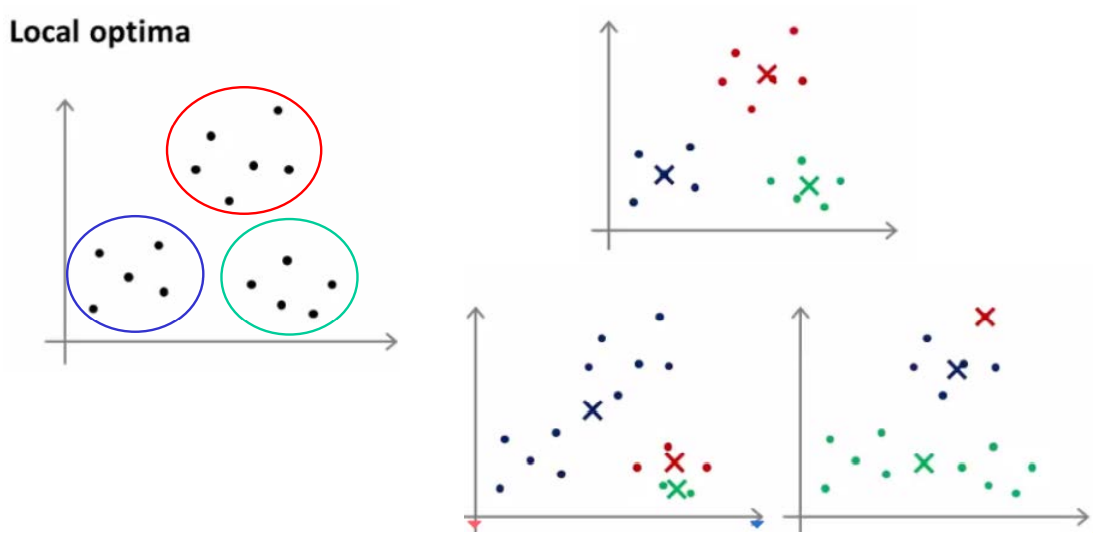
Random initialization 방법의 경우 데이터 들 중 K개를 Centroid로 사용하므로 다양한 결과가 발생할 수 있다. 이는 발생할 수 있는 모든 경우가 global optimum이 아니라는 의미이고 잘못된 initialization을 통한 결과는 local optimum에 빠질 수 있다는 것을 의미한다. 따라서 K-means clustering에 있어 initialization이 중요하다는 것을 알 수 있다.

이를 해결하기 위한 방법이 바로 multiple random initialization이다. random initialization을 통한 K-means Clustering을 여러 번 돌려 각각의 결과에 대한 Cost 값을 모두 저장하고 , 가장 Cost 값이 낮은 것을 선택하겠다는 것이다. 2 ~ 10 사이의 작은 K에서는 random initialization에 비해 multiple random initialization이 좋은 효과를 보인다. 하지만 11 이상의 K에서는 multiple random initialization과 random initialization의 결과가 크게 차이 나지 않는다. 즉 이미 첫 번째 initialization의 결과가 괜찮게 나왔을 가능성이 높다는 것이다. K가 크다는 것은 그만큼 random initialization에 영향을 덜 받는다는 이야기이고 , local optimum 빠질 확률이 낮다는 것이다.

K-means Clustering의 목적함수는 다음과 같다. 각 데이터 포인트들과 해당 Cluster의 Centroid까지의 거리를 모두 더하고 이 더한 값이 최소가 되도록 하는 것이 목표이다. K-means Clustering의 목표는 모든 데이터 포인트에 대해서 Centroid와의 거리가 최소가 될 수 있는 Centroid를 찾는 것이 목표이므로 목적함수는 위와 같은 식으로 표현된다.
위에서 K-means Clustering의 K는 모델의 목적에 따라서 정할 수 있다고 하였다. K의 개수가 중요하지 않은 경우 최적의 K는 어떻게 구할 수 있을까. 이에 대하여 사용할 수 있는 한 가지 방법으로 Elbow method가 존재한다.
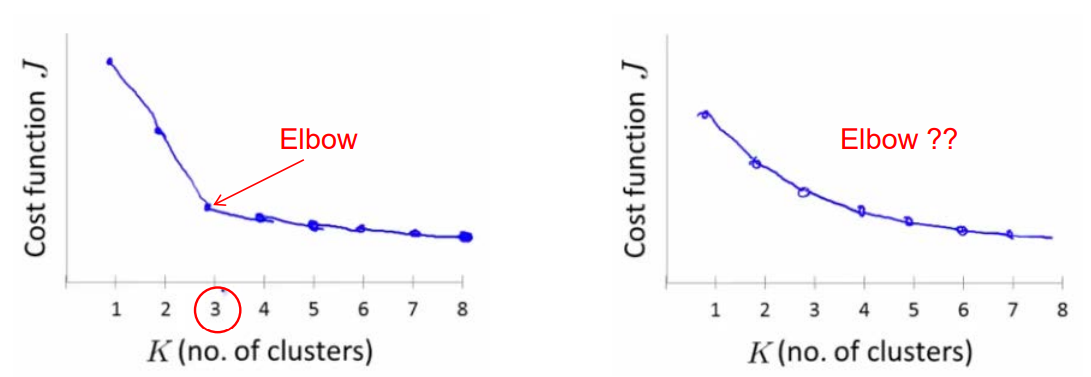
Elbow method의 경우 Cost function의 값들을 가능한 K에 대하여 모두 구하고 이를 통해 Elbow Point를 찾는 것이 목표이다. 위의 그래프에서도 알 수 있듯이 K의 개수가 늘어날수록 Cost function의 값을 줄어들 수밖에 없다. Cluster의 개수인 K와 데이터의 개수인 N이 같아지게 된다면 하나의 데이터에 하나의 Centroid가 들어가게 될 것이고 Cost function의 값은 0이 될 것이다.
위의 그래프에서 볼 수 있듯이 , Cost function이 급격하게 변하는 Elbow Point를 찾을 수 있다. 이는 이 Elbow Point 이상으로 K를 늘리는 것은 이점이 없음을 의미하며 새로운 Cluster에 데이터가 많이 속하지 않는다는 것을 의미한다. 따라서 Elbow method는 K를 정하는 것에 대한 판단 기준이 될 수 있다. 하지만 언제나 Elbow Point가 존재하는 것이 아닐뿐더러 , 언제나 Elbow Point가 최적의 K가 될 수는 없다. 위에서 살펴본 것처럼 분석의 목표에 따라 K를 정하는 것이 가장 좋다.
'코딩 > 데이터 분석 이론 & 응용' 카테고리의 다른 글
| [6] Deep Learning - Neural Network (0) | 2022.01.09 |
|---|---|
| [5] Co-Occurrence Networks Analyzing (0) | 2022.01.08 |
| [4] Latent Semantic Analysis & SVD (1) | 2022.01.08 |
| [3] Predicting Forest Cover with Decision Trees (0) | 2022.01.07 |
| [1] Collaborating Filtering & Alternating Least Squares (0) | 2022.01.05 |



